Трещиностойкость (вязкость разрушения)

Прогнозирование трещиностойкости хрупких материалов методом индентирования предусматривает растрескивание от контакта с индентором, ведь трещины являются наиболее важным фактором трещиностойкости. Однако, вовремя индентирования пластичных материалов, таких как металлы, растрескивание не происходит. По этой причине чтобы использовать метод индентирования для расчета трещиностойкости пластичных материалов, следует принять критерий критической точки разрушения при вдавливании, соответствующий началу нестабильного роста трещины, такой как критическое разрушающее напряжение, критическая деформация при разрушении и критическая доля свободного объема. Ввиду схожести состояния напряжения, трещиностойкость пластичного материала можно рассчитать с помощью метода инструментального индентирования.
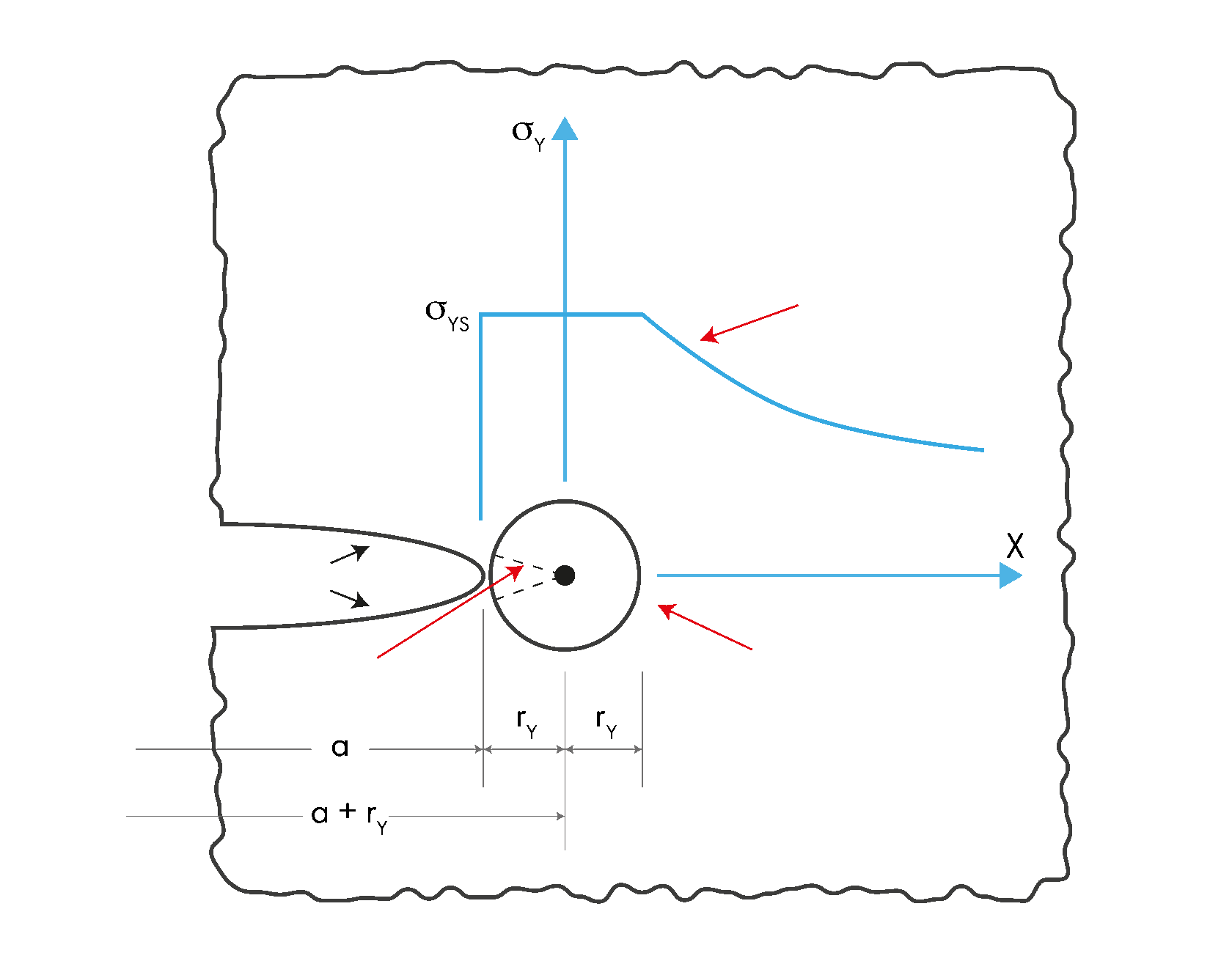
Концентрация напряжения, создаваемая с помощью сферического наконечника индентора аналогична концентрации перед вершиной трещины. Таким образом, материал под сферическим наконечником индентора в высокой степени подвержен поперечному сжатию окружающего упругого материала, и этот эффект на определенной глубине вдавливания аналогичен воздействию перед острым надрезом. Хотя вдавливание на определенную критическую глубину отвечает условиям возникновения трещины, эффект поперечного сжатия может быть достаточно сильным, чтобы подавить образование трещины в пластичном материале во время вдавливания. Таким образом, трещиностойкость можно прогнозировать, определяя критическую глубину вдавливания, соответствующую началу нестабильного роста трещины.
С точки зрения энергии, энергия, необходимая для начала разрушения, может быть выражена как энергия деформации при вдавливании, поглощенная на каждую единицу площади до критической глубины вдавливания.
Схематическая иллюстрация упругопластического отклика на вдавливание

Упругая деформация

Упругопластическая (переход) деформация

Полностью пластическая деформация
Для построения расчетной модели трещиностойкости методом инструментального индентирования используются концепции критического разрушающего напряжения и критической деформации при разрушении для хрупких и вязких материалов соответственно. Модель предполагает, что хрупкое разрушение, т. е. хрупкий излом, происходит, когда локальное напряжение растяжения при вдавливании превышает критическое значение, которое рассматривалось с точки зрения течения деформации при вдавливании. И наоборот, предполагается, что вязкое разрушение происходит, когда в испытаниях на растяжение локальная деформация достигает деформации разрушения, установленной по свойствам материала, определенным путем измерительного индентирования. Наконец, каждый критерий разрушения используется для определения энергии разрушения при вдавливании, которая соответствует энергии разрушения, необходимой для роста трещины.
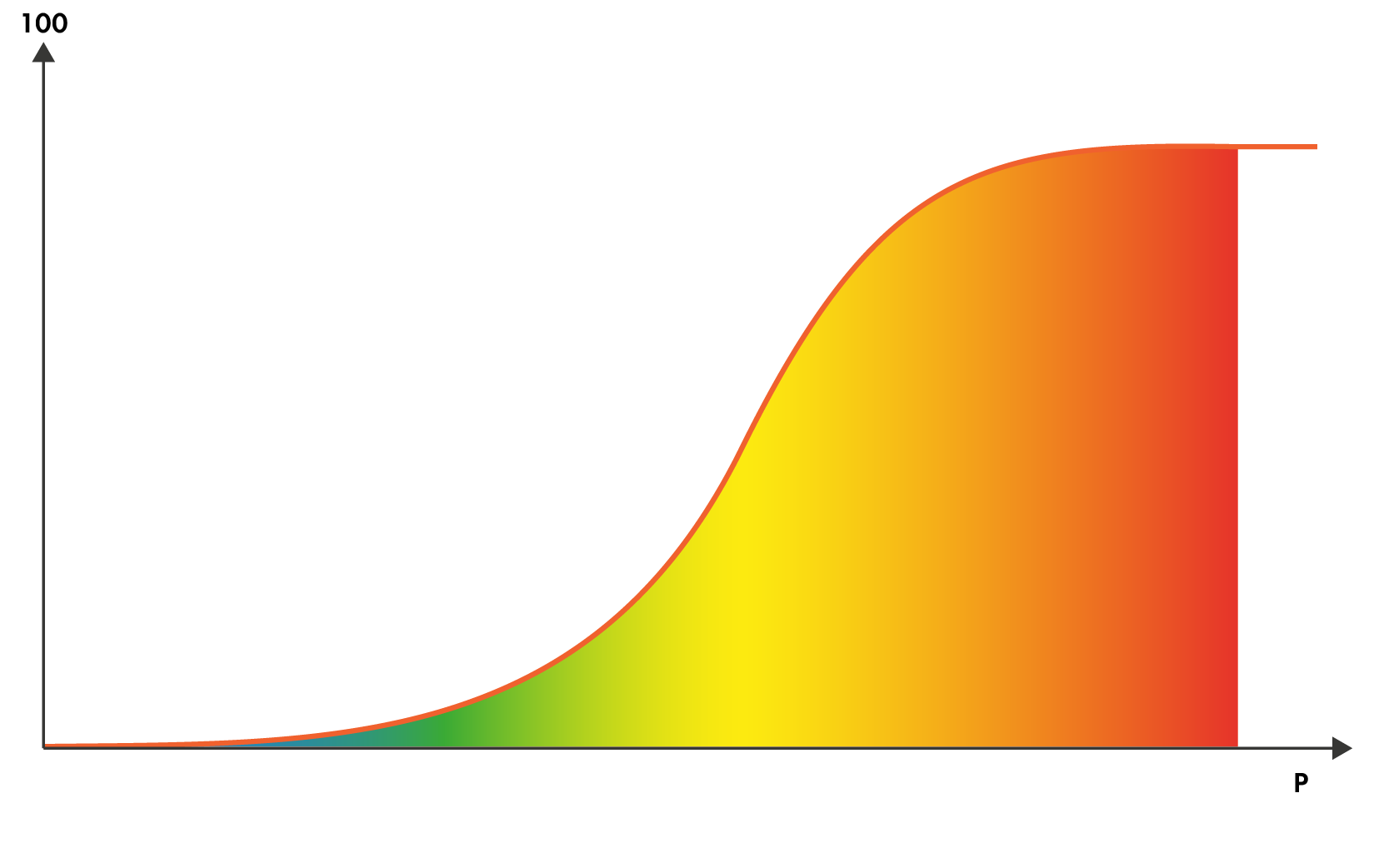
Доля пластической деформации, %
Упругая деформация
Пластическая деформация
Два этапа пластической деформации хрупкого разрушения






Этап 1
Этап 2
Исключительно упругая деформация
Зарождающаяся пластичность
Упруго-пластическая деформация
В основном пластическая деформация
Начало роста полностью пластической зоны
Развитие трещины
Поверхности трещины
Индентор
Рост трещины
Зона идеальной пластичности
\(\sigma_{y}=\sqrt{x}\)= константа
Распределение эластичного напряжения
Распределение эластичного напряжения
Зона пластичности
Зона эластичности
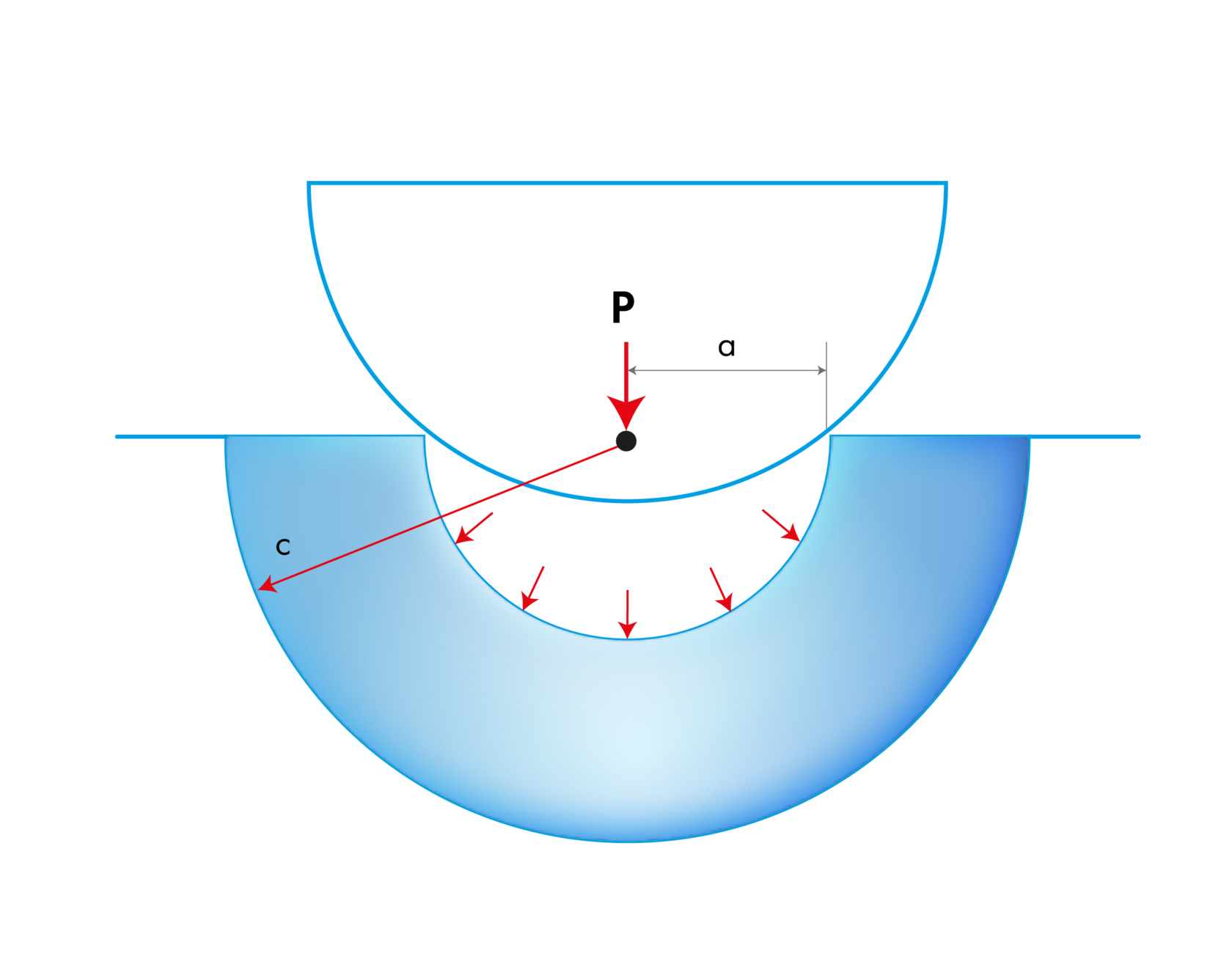
Трещиностойкость \( K_{JC}\) в бесконечной плоскости длиной \(2a\) рассчитывается с помощью уравнения:
\[K_{JC}=\sigma_{f}\sqrt{\pi a},\]
где \(\sigma_{f}\) — дистанционное напряжение растяжения при разрушении согласно теории Гриффита выражается уравнением:
\[\sigma_{f}=\sqrt{\frac{2E\omega_{f}}{\pi a}}\]
объединив эти 2 уравнения получаем:
\[\sigma_{f}=\sqrt{E_{0}\lim_{h \rightarrow h^{*}}\int_{0}^{h}\frac{F}{A_{c}}dh}=\sqrt{\frac{E_{0}}{\pi}}k^{\prime} \ln\left(\frac{2R}{2R-h^{*}}\right),\]
где \(k^{\prime}\) — наклон (\(F_{max}/h_{max}\)) между максимальной нагрузкой вдавливания и максимальной глубиной вдавливания на кривой разгрузки;
\(A_{c}\) — площадь поверхности контакта между материалом и индентором;
F — нагрузка вдавливания;
h — глубина вдавливания;
\(h^{*}\) — характеристическая точка начала разрушения по глубине вдавливания.
Расчет характеристической точки начала разрушения (\(h^{*}\)) по глубине вдавливания производится с помощью критического модуля упругости:
\[h^{*}= \exp\left(\frac{1nE^{*}-A}{B}\right),\]
где \(E^{*}\) — критический модуль упругости.
B — наклон кривой, полученной приближением.
\[E^{*}=E_{0}(1-D)\]
\(E_{0}\) – модуль упругости исходного материала, определяется на основании эффективного модуля упругости и приведенного модуля упругости определяемых на множестве кривых разгрузки.
Приведенный модуль упругости:
\[E_{r}=\frac{\sqrt{\pi}}{2}S\frac{1}{\sqrt{A_{c}}},\]
где S – наклон кривой разгрузки
Эффективный модуль упругости на основании приведенного модуля упругости:
\[E_{eff}=\frac{1-\upsilon^{2}}{\left(\frac{1}{E_{r}}-\frac{1-\upsilon_i^2}{E_{I}}\right)}+\frac{1-\upsilon^{2}}{\left(\frac{2\sqrt{A_{C}}}{\sqrt{\pi S}}-\frac{1-\upsilon_i^2}{E_{I}}\right)},\]
где v и \(v_{i}\) — коэффициент Пуассона материала и индентора соответственно;
\(E_{r}\) — приведенный модуль упругости; \(E_{i}\)— модуль упругости головки индентора.
Расчет параметра повреждения (D) связан поверхностной плотностью микродефектов в материале и определяется на основе доли свободного объема (f) производится с помощью уравнения:
\[D=\frac{\pi}{\left(\frac{4}{3}\pi \right)^{\frac{2}{3}}}f^{\frac{2}{3}};\]
\[K_{JC}=\sigma_{f}\sqrt{\pi a},\]
где \(\sigma_{f}\) — дистанционное напряжение растяжения при разрушении согласно теории Гриффита выражается уравнением:
\[\sigma_{f}=\sqrt{\frac{2E\omega_{f}}{\pi a}}\]
объединив эти 2 уравнения получаем:
\[\sigma_{f}=\sqrt{E_{0}\lim_{h \rightarrow h^{*}}\int_{0}^{h}\frac{F}{A_{c}}dh}=\sqrt{\frac{E_{0}}{\pi}}k^{\prime} \ln\left(\frac{2R}{2R-h^{*}}\right),\]
где \(k^{\prime}\) — наклон (\(F_{max}/h_{max}\)) между максимальной нагрузкой вдавливания и максимальной глубиной вдавливания на кривой разгрузки;
\(A_{c}\) — площадь поверхности контакта между материалом и индентором;
F — нагрузка вдавливания;
h — глубина вдавливания;
\(h^{*}\) — характеристическая точка начала разрушения по глубине вдавливания.
Расчет характеристической точки начала разрушения (\(h^{*}\)) по глубине вдавливания производится с помощью критического модуля упругости:
\[h^{*}= \exp\left(\frac{1nE^{*}-A}{B}\right),\]
где \(E^{*}\) — критический модуль упругости.
B — наклон кривой, полученной приближением.
\[E^{*}=E_{0}(1-D)\]
\(E_{0}\) – модуль упругости исходного материала, определяется на основании эффективного модуля упругости и приведенного модуля упругости определяемых на множестве кривых разгрузки.
Приведенный модуль упругости:
\[E_{r}=\frac{\sqrt{\pi}}{2}S\frac{1}{\sqrt{A_{c}}},\]
где S – наклон кривой разгрузки
Эффективный модуль упругости на основании приведенного модуля упругости:
\[E_{eff}=\frac{1-\upsilon^{2}}{\left(\frac{1}{E_{r}}-\frac{1-\upsilon_i^2}{E_{I}}\right)}+\frac{1-\upsilon^{2}}{\left(\frac{2\sqrt{A_{C}}}{\sqrt{\pi S}}-\frac{1-\upsilon_i^2}{E_{I}}\right)},\]
где v и \(v_{i}\) — коэффициент Пуассона материала и индентора соответственно;
\(E_{r}\) — приведенный модуль упругости; \(E_{i}\)— модуль упругости головки индентора.
Расчет параметра повреждения (D) связан поверхностной плотностью микродефектов в материале и определяется на основе доли свободного объема (f) производится с помощью уравнения:
\[D=\frac{\pi}{\left(\frac{4}{3}\pi \right)^{\frac{2}{3}}}f^{\frac{2}{3}};\]
Доля свободного объема
f – для хрупких материалов лежит в диапазоне от 0,13 до 0,17;
f – для вязких материалов лежит в диапазоне от 0,23 до 0,27

